1. Notasi dan Penggambaran Vektor
Notasi vektor dapat berupa huruf kapital atau huruf kecil. Sebuah vektor dalam buku cetakan biasanya dinyatakan dalam lambang huruf besar yang dicetak tebal, misalnya: A atau B. Untuk tulisan tangan vektor biasa dilambangkan dengan sebuah huruf kecil yang diberi tanda anak panah di atasnya.
Penulisan nilai atau besar vektor pada buku cetakan biasanya menggunakan huruf besar miring (italic), seperti A atau B, sedangkan tulisan tangan dinyatakan dengan huruf tanpa tanda panah A atau sebuah huruf besar dengan anak panah di atasnya beserta tanda harga mutlak
.
Besar vektor diwakili panjang anak panah. Semakin panjang gambar sebuah vektor, semakin besar nilai vektor tersebut. Sebuah vektor dikatakan negatif apabila mempunyai arah yang berlawanan dengan vektor yang dijadikan acuan. Dua buah vektor dikatakan sama jika besar dan arahnya sama. sedangkan dua buah vektor dikatakan berlawanan jika besarnya sama tetapi arahnya berlawanan.
2. Resultan Vektor
Resultan vektor adalah hasil penjumlahan atau pengurangan dua vektor atau lebih. Resultan vektor dapat diperoleh dengan beberapa metode, yaitu metode segitiga, metode jajargenjang, poligon, dan analitis.
a.resultan vektor dengan metode segitiga
Untuk mengetahui jumlah dua buah vektor Anda dapat menggunakan metode segitiga.
Langkah-langkahnya adalah sebagai berikut.
1) Gambarlah vektor pertama sesuai dengan nilai dan arahnya, disini kami akan menuliskan vektor A
2) gambar vektor kedua, misalnya B, sesuai nilai dan arahnya dengan titik tangkapnya berimpit pada ujung vektor pertama
3) Hubungkan titik tangkap vektor pertama (A) dengan ujung vektor kedua (B)!
Selisih dua buah vektor dapat diketahui dengan cara seperti penjumlahan vektor. Misalnya, selisih dua buah vektor A dan B adalah C, juga dapat dinyatakan C = A – B atau C = A + (-B). Hal tersebut menunjukan bahwa selisih antara vektor A dan B adalah hasil penjumlahan vektor A dan -B, dengan -B adalah vektor yang berlawanan arah dengan B tetapi nilainya sama dengan B.
Perhatikan ilustrasi vektor berikut
b. resultan vektor dengan Metode Jajargenjang
Anda dapat memperoleh resultan dua buah vektor dengan metode jajargenjang.
Pada metode jajargenjang terdapat beberapa langkah, yaitu sebagai berikut.
1) Gambar vektor pertama dan vektor kedua dengan titik pangkal berimpit
2) gambarlah sebuah jajargenjang dengan kedua vektor tersebut sebagai sisi-sisinya
3) Resultan kedua vektor adalah diagonal jajargenjang yang titik pangkalnya sama dengan titik pangkal kedua vektor.
Pada metode jajargenjang, satu kali menggambar jajargenjang hanya dapat digunakan untuk mencari resultan dua buah vektor. Untuk resultan yang terdiri atas tiga buah vektor diperlukan dua jajargenjang, empat buah vektor diperlukan tiga jajargenjang, dan seterusnya.
c. Metode Poligon
Metode poligon dapat digunakan untuk menjumlahkan dua buah vektor atau lebih, metode ini merupakan pengembangan dari metode segitiga.
Langkah-langkah menentukan resultan beberapa vektor dengan metode poligon adalah sebagai berikut.
1) Gambar vektor pertama.
2) Gambar vektor kedua dengan pangkalnya berimpit di ujung vektor pertama.
3) Gambar vektor ketiga, dengan pangkalnya berimpit di ujung vektor kedua dan seterusnya hingga semua vektor yang akan dicari resultannya telah digambar.
4) Gambar vektor yang menghubungkan pangkal vektor pertama dengan ujung dari vektor terakhir.
5) Vektor resultan atau vektor hasil penjumlahannya adalah vektor yang menghubungkan pangkal vektor pertama dengan ujung dari vektor yang terakhir digambar.
d. Metode Analisis
Metode yang paling baik (tepat) untuk menentukan resultan beberapa vektor dan arahnya adalah metode analisis. Metode ini, mencari resultan dengan cara perhitungan bukan pengukuran, yaitu menggunakan rumus kosinus dan mencari arah vektor resultan dengan menggunakan rumus sinus.
1) Menentukan Resultan Vektor Menggunakan Rumus Kosinus
Untuk menentukan vektor resultan secara matematis dapat digunakan rumus kosinus, yaitu sebagai berikut.
Keterangan:
R : resultan vektor
F1 : vektor pertama
F1 : vektor kedua
q: sudut apit antara kedua vektor
2) Menentukan Arah Resultan Vektor Menggunakan Rumus Sinus
Seperti yang kita ketahui bahwa vektor merupakan besaran yang mempunyai nilai dan arah. Untuk menentukan arah dari vektor resultan terhadap salah satu vektor komponennya dapat digunakan persamaan sinus.
Diketahui dua buah vektor, F1 dan F2 membentuk sudut a. Sudut antara vektor resultan (R) dengan vektor F1 adalah b, sedangkan sudut antara resultan (R) dan vektor F2 adalah a- b.
Secara matematis persamaan tersebut dapat ditulis sebagai berikut.
3. Menguraikan Vektor berdasarkan komponennya
Setelah memahami cara menjumlahkan vektor, kita akan mempelajari cara menguraikan sebuah vektor. Sebuah vektor dapat diuraikan menjadi dua buah vektor atau lebih. Pada materi ini, kita hanya akan mempelajari cara menguraikan sebuah vektor menjadi dua buah vektor yang saling tegak lurus, yaitu pada sumbu X dan sumbu Y.
a. Menentukan Komponen Sebuah Vektor yang Besar dan Arahnya Diketahui
Vektor komponen adalah dua buah vektor atau lebih yang menyusun sebuah vektor. Setiap vektor dapat diuraikan menjadi dua buah vektor yang saling tegak lurus.
Misalkan, sebuah vektor F yang dapat diuraikan menjadi vektor komponen pada sumbu X, yaitu FX dan vektor komponen pada sumbu Y, yaitu Fy. Jika sudut antara vektor F dengan sumbu X positif adalah q, maka besar vektor komponen FX dan Fy dapat Anda peroleh dengan menggunakan persamaan sinus dan kosinus.
FX = F cosq
Fy = F sinq
b. Menentukan Besar dan Arah Sebuah Vektor Jika Kedua Vektor Komponennya Diketahui
Misalkan, jika komponen-komponen vektor F adalah Fx dan Fy, maka besar vektor F dapat ditentukan dengan menggunakan dalil Phytagoras pada segitiga siku-siku. Arah vektor tersebut dapat ditentukan dengan menggunakan perbandingan trigonometri tangen.
Besar vektor F adalah sebagai berikut.
Arah vektor F adalah sebagai berikut.
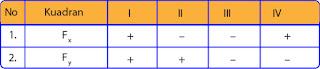
Untuk menentukan arah vektor (sudut yang dibentuk terhadap sumbu X positif) kita harus memperhatikan tanda Fx dan Fy, tanda tersebut akan membantu Anda dalam menentukan kuadran dalam vektor koordinat.
Berikut ini tabel nilai Fx dan Fy pada masing-masing kuadaran;














EmoticonEmoticon