Gerak Lurus Berubah Beraturan(GLBB)
Gerak lurus berubah beraturan adalah gerak dengan lintasan dan percepatan tetap.
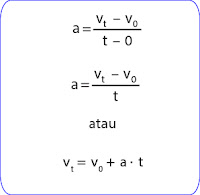
Percepatannya adalah
Jika pada saat t1 = 0 benda telah memiliki kecepatan vo dan pada saat t2 = t benda memiliki kecepatan vt, maka persamaannya menjadi seperti berikut.
Benda yang bergerak dengan percepatan tetap menunjukkan kecepatan benda tersebut bertambah secara beraturan. Oleh karena itu, jika diketahui kecepatan awal dan kecepatan akhir, maka kecepatan rata-rata benda sama dengan separuh dari jumlah kecepatan awal dan kecepatan akhir.
Jika s merupakan perpindahan yang ditempuh benda dalam interval waktu (t), maka persamaan menjadi sebagai berikut.
Selanjutnya, untuk dapat menentukan kecepatan akhir sebuah benda yang mengalami percepatan tetap pada jarak tertentu dari kedudukan awal tanpa mempersoalkan selang waktunya, variabel t dapat ‘dihilangkan’ dengan mensubstitusikan persamaan t=(vt – v0)/a (diperoleh dari persamaan vt = v0 + a · t) ke dalam persamaan diatas
Grafik hubungan v dan t serta s dan t pada gerak lurus berubah beraturan (GLBB) adalah sebgai berikut.
1. Grafik (v - t)
Berdasarkan persamaan vt = v0 + a · t, Grafik hubungan antara v dan t dapat dilukiskan sebagai berikut.
Grafik pada diatas menunjukkan bahwa perpindahan yang ditempuh benda (s) dalam waktu (t) sama dengan luas daerah di bawah grafik yang dibatasi oleh sumbu v dan t (daerah yang diarsir).
s = luas trapesium OABD = luas segi empat OACD + luas segitiga ABC
2. Grafik (s - t)
Grafik hubungan antara s dan t dapat digambarkan sebagai berikut sebagai berikut.
Gerak lurus diperlambat beraturan
Persamaan-persamaan GLBB di atas merupakan persamaan untuk gerakan dipercepatan beraturan.
Untuk Rumus-rumus GLBB yang diperlambat adalah sebagai berikut.
Gerak Jatuh Bebas
Gerak jatuh bebas adalah gerak sebuah benda yang jatuh dari ketinggian tertentu tanpa kecepatan awal. Contoh gerak jatuh bebas adalah apel yang jatuh dari pohonnya. Dalam gerak jatuh bebas gaya gesekkan udara diabaikan atau dengan kata lain tidak ada gaya luar yang mendorong atau menghambat gerak jatuh tersebut.
Gerak jatuh secara ideal dapat diamati pada benda yang dijatuhkan dalam ruang hampa udara sehingga tidak ada pengaruh gaya apung dan gesekan udara. Gerak jatuh dalam ruang hampa udara membuktikan bahwa benda jatuh tidak ditentukkan oleh bentuk dan massanya.
Jika sebuah benda jatuh bebas dengan kecepatan awal Vo = 0, persamaan kecepatan benda tersebut adalah
Jarak vertikal ke bawah yang ditempuh benda setelah t sekon dinyatakan dengan persamaan berikut ini
dengan:
v= besarnya kecepatan benda (m/s)
s = jarak yang ditempuh benda (m)
t = waktu tempuh (s)
sebuah benda jatuh bebas dari ketinggian ho meter di atas tanah. Untuk sampai di permukaan tanah, berda tersebut membutuhkan waktu tempuh t sekon. Dengan demikian dapat diturunkan persamaan berikut
ht= ho-s
ketika benda mencapai tanah, ht = 0 maka
dengan
t= waktu tempuh(s)
h = ketinggian benda mula-mula(m)
g = percepatan gravitasi (m/s2)
laju benda saat menyentuh tanah adalah
Gerak Vertikal Ke Atas
Jika sebuah benda dilemparkan vertikal keatas maka sepanjang lintasan lurusnya bola tersebut selalu mengalami percepatan gravitasi bumi yang arahnya ke bawah. Gerak vertikal ke atas dan gerak vertikal ke bawah memiliki percepatan gravitasi yang sama besar. Gerak vertikal ke atas berupa gerak diperlambat karena semakin ke atas kecepatannya semakin berkurang. Pada ketinggian maksimum, kecepatan bola menjadi nol(vt = 0). Pada keadaan itu bola berhenti sesaat lalu jatuh bebas kebawah. Rumus yang digunakan pada gerak lurus juga berlaku untuk gerak vertikal ke atas dan gerak jatuh bebas.
Persamaan yang berlaku pada gerak vertikal ke atas adalah sebagai berikut:
dengan:
h = ketinggian benda dari kedudukan awal (m)
vo = kecepatan awal (m/s)
g = percepatan gravitasi (m/s2)
t = waktu tempuh (s)
vt = kecepatan pada t sekon (m/s)
sebuah benda yang dilemparkan vertikal ke atas, lalu jatuh dan kembali ketitik semula memiliki jarak tempuh yang sama dengan panjang lintasan yang dilalui benda selam bergerak. Akan tetapi, benda tidak memiliki harga perpindahan atau besar perpindahannnya sam dengan nol;
waktu yang dibutuhkan sepanjang lintasan adalah sebagai berikut.
Karena arah percepatan (gravitasi) berlawanan arah dengan arah pergerakan benda, maka suatu saat kecepatan benda yang bergerak vertikal ke atas akan sama dengan nol. Ketika kecepatannya sama dengan nol, benda tersebut telah mencapai ketinggian maksimum. Bagaimana cara menghitung ketinggan maksimum benda yang bergerak vertikal ke atas?
Rumus mencari ketinggian maksimum adalah sebagai berikut
Mencari waktu untuk mencapai ketinggian maksimum
Subtitusikan persamaan tersebut pada rumus mencari ketinggian benda, sehingga
dengan:
hmaks = tinggi maksimum (m)
vo = kecepatan awal (m/s)
g = percepatan gravitasi (m/s2)



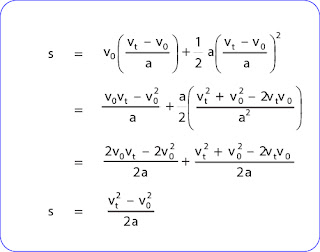



















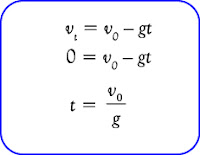


EmoticonEmoticon