Vektor Satuan
Vektor satuan adalah vektor yang mempunyai besar/nilai 1, dan tidak memiliki satuan. Penjumlahan dalam vektor sering kali dinyatakan dalam sebuah vektor satuan. Vektor satuan digunakan semata-mata hanya untuk menunjukkan arah. Simbol dari vektor satuan adalah

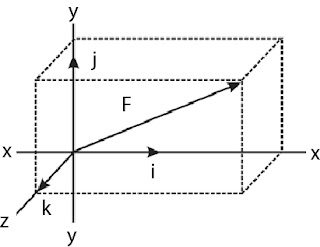
yang menunjukan arah positif sumbu x, sumbu y, sumbu z(vektor biasanya dituliskan dengan tanda 'topi' atau hat). Dalam sistem koordinat, Ketiga vektor satuan tersebut saling tegak lurus satu sama lain. Seperti yang ditunjukkan gambar berikut:
Nilai atau besar setiap vektor satuan sama dengan 1, atau dapat dituliskan nilai mutlak
= 1.
Misalkan ada sebuah vektor F yang terletak pada ruang,
kemudian diproyeksikan menjadi komponen vektor Fx, Fy, dan Fz. Maka Vektor F dapat dinyatakan dalam penjumlahan dari tiga buah vektor yaitu:
Besar vektor F dapat dihitung dengan cara menentukan komponen-komponen vektor yang saling tegak lurus satu sama lain melalui persamaan berikut ini
Dua buah vektor sama jika besar komponen-komponennya juga sama. sebagai contohnya
Besar resultan Vektor tersebut dapat dinyatakan dengan aturan berikut ini:
Besar resultan penjumlahan vektor
Sedangan besar resultan pengurangan vektor adalah sebagai berikut:
Perkalian Vektor
Selain operasi penjumlahan dan pengurangan vektor, operasi perkalian juga dapat diterapkan pada vektor. Akan tetapi perkalian vektor tidak sama dengan perkalian biasa. Terdapat dua jenis perkalian Vektor, yaitu perkalian titik(dot) vektor dan perkalian silang vektor.
Perkalian titik (dot) vektor
Misal ada dua buah vektor A dan B. Perkalian titik vektor A dan vektor B adalah besar vektor A dikalikan dengan komponen vektor B pada arah vektor A. Karena proyeksi dari kompenen vektor B pada arah A adalah B cos f, maka juga dikatakan bahwa perkalian titik antara dua vektor A dan Vektor B merupakan besaran skalar yang besarnya sama dengan hasil kali kedua vektor terhadap cosinus sudut apitnya.
Secara matematis dapat dituliskan
Hasil dari perkalian titik vektor adalah besaran skalar dan perkalian titik vektor juga biasa disebut dengan perkalian skalar.
Jika f diantara 0o-90o maka cos f> 0 sehingga hasilnya positif
Jika f diantara 90o-180o maka cos f< 0 sehingga hasilnya negatif
Jika f = 90o maka cos f = 0 sehingga hasilnya nol (0).
Cara menghitung perkalian skalar vektor dengan komponen vektor
Perkalian skalar vektor dapat dihitung secara langsung jika komponen x , y, dan z dari vektor-vektor tersebut diketahui.
Caranya kita nyatakan vektor A dan vektor B ke dalam bentuk komponen-komponennya, kemudian dijabarkan dengan vektor satuan.
Berdasarkan persamaan diatas, didapatkan rumus untuk menentukkan sudut kedua vektor:
Perkalian silang vektor
Cara menentukkan perkalian vektor A x B adalah dengan menggambarkan Vektor A dan B pada bidang yang sama, dan pangkal kedua vektor saling berhimpit. Maka vektor hasil perkaliannya tegak lurus bidang tersebut dan besarnya sama dengan ABsinf.
Atau juga bisa dikatakan
Perkalian silang dua buah vektor A x B menghasilkan vektor yang arahnya tegak lurus bidang yang dibentuk oleh dua buah vektor tersebut, dan besarnya sama dengan hasil kali kedua vektor dengan sinus sudut apitnya.
Secara matematis perkalian silang vektor dapat dituliskan:
Jika digambarkan maka menjadi seperti berikut
Pada perkalian silang vektor tidak berlaku sifat komutatif tetapi berlaku sifat anti komutatif:
Untuk menentukkan nilai resultan vektor dan persamaan perkalian vektor, dapat digunakan sifat perkalian silang sesama satuan yaitu perkalian dua vektor satuan yang berbeda akan bernilai positif jika searah jarum jam, sebaliknya akan bernilai negatif jika arahnya berlawanan dengan arah jarum jam.
Jika kedua vektor tersebut sejajar atau atau anti sejajar maka vektor hasilnya adalah 0.
Cara lain yang lebih sederhana untuk menghitung perkalian silang dua vektor A dan B adalah dengan menggunakan metode determinan.












EmoticonEmoticon