1. Ukuran Sudut (Derajat dan Radian)
Ada dua ukuran yang umum digunakan untuk menentukan besar suatu
sudut, yaitu derajat dan radian. 1O
didefinisikan sebagai besar sudut yang dibentuk oleh 1/360 putaran penuh atau
jika diartikan sebaliknya maka 1 putaran penuh = 360 derajat. Satu radian
diartikan sebagai ukuran sudut pusat a suatu lingkaran yang
panjang busurnya sama dengan jari-jari.
Hubungan derajat dan radian adalah sebagai berikut:
Contoh:
2. Perbandingan Trigonometri Pada Segitiga Siku-Siku
Sinus suatu sudut didefinisikan sebagai perbandingan panjang sisi di depan
sudut dengan sisi miring,
Cosinus suatu sudut didefinisikan sebagai perbandingan panjang sisi disamping
sudut dengan sisi miring
Tangen suatu sudut didefinisikan sebagai perbandingan panjang sisi di depan
sudut dengan sisi di samping sudut,
Cosecan suatu sudut didefinisikan sebagai panjang sisi miring dengan sisi di
depan sudut,
Secan suatu sudut didefinisikan sebagai perbandingan panjang sisi miring dengan
sisi di samping sudut
Cotangen suatu sudut didefinisikan sebagai perbandingan sisi di samping sudut
dengan sisi di depan sudut
3. Nilai Perbandingan Trigonometri di Berbagai Kuadran
Nilai
perbandingan trigonometri di setiap kuadran, yaitu:
a. Jika di kuadran I, maka
nilai sinus, cosinus, dan tangen bertanda positif.
b. Jika di kuadran II, maka
nilai sinus bertanda positif dan nilai cosinus dan tangen bertanda negatif.
c. Jika di kuadran III, maka nilai tangen bertanda positif dan nilai sinus dan
cosinus bertanda negatif.
d. Jika di kuadran IV, maka
nilai cosinus bertanda positif dan nilai sinus dan tangen bertanda negatif.
4. Perbandingan Trigonometri Sudut-sudut Istimewa
Sudut
istemewa
dalam trigonometri artinya sudut-sudut yang
nilai perbandingan trigonometri dapat ditentukan secara eksak. Sudut
istimewa di kuadran I contohnya 30° dan
45°.
Berikut ini nilai perbandingan trigonometri untuk semua sudut-sudut
istimewa.
5. Penggunaan
Rumus Trigonometri
untuk Jumlah dan Selisih Dua
Sudut:
a. Rumus Cosinus Jumlah dan Selisih
Dua Sudut
Rumus cosinus
jumlah dua sudut:
cos (A + B) = cos A cos B – sin A sin B
Rumus cosinus
selisih dua sudut:
cos (A – B) = cos A cos B + sin A sin B
b. Rumus Sinus Jumlah dan Selisih Dua
Sudut
Rumus
sinus jumlah dua sudut:
sin (A + B) = sin A cos B + cos A sin B
Rumus sinus selisih dua sudut:
sin (A – B) = sin A cos B – cos A sin B
c. Rumus Tangen Jumlah dan Selisih Dua Sudut
Contoh:
1.Hitunglah
sin 15O !
Jawab:
2.Hitunglah
Tan 105O !
Jawab:
3. Jika Sin a = 4/5 dan
cos b = 7/25 dengan 0 ≤ a ≤p/2 dan 0 ≤ a ≤p/2, tentukan nilai sin (a+b) dan cos
(a-b)
Jawab:
Sin a = 4/5, maka cos a = 3/5
Cos b = 7/25 , maka sin b = 24/25
Sehingga:
6. Penggunaan Rumus Sinus, Cosinus, dan Tangen Sudut Ganda
a. Menggunakan Rumus Sinus Sudut Ganda
Berdasarkan rumus sin (A + B), untuk A = B maka diperoleh:
sin 2A = sin (A + A)
= sin A cos A + cos A sin A
= 2 sin A cos
A
b. Rumus Cosinus Sudut Ganda
Dengan
menggunakan rumus cos (A + B), untuk A = B maka
diperoleh:
cos 2A = cos (A + A)
= cos A cos A – sin A sin A
= cos2 A –
sin2 A
Ingat
bahwa sin2 A +
cos2 A = 1
Maka cos 2A dapat dituliskan
cos 2A = cos2 A – sin2 A
= cos2
A – (1 – cos2 A)
= cos2
A – 1 + cos2 A
= 2 cos2 A
– 1
Atau
cos 2A = cos2 A – sin2 A
= (1 – sin2
A) – sin2 A
= 1 – 2 sin2 A
Sehingga rumus cosinus untuk sudut ganda yaitu
cos 2A = cos2 A – sin2 A
cos 2A = 2 cos2 A – 1
cos 2A = 1 –
2 sin2 A
c. Rumus Tangen Sudut Ganda
Rumus sudut ganda untuk tangen yaitu:
Contoh:
Hitunglah nilai sin 120 o !
Jawab:
sin120o
= sin 2(60o )
= 2sin 30o cos30o
= 2 x ½ x ½Ö3
= ½ Ö3
d. Rumus Trigonometri untuk sin ½ A, cos ½ A, dan tan ½ A
7. Perkalian
Sinus dan Cosinus dalam Jumlah atau Selisih Sinus atau Cosinus
b. Perkalian Sinus dan Sinus
Dari rumus
jumlah dan selisih dua sudut, dapat diperoleh rumus sebagai berikut:
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
Jika ruas yang bersesuaian kita kurangkan maka akan diperoleh
cos (A + B) – cos (A –B) = –2 sin A sin B
atau juga dapat
dituliskan:
2 sin A sin B = cos (A – B) – cos (A + B)
a. Perkalian Cosinus dan Cosinus
Dari rumus
jumlah dan selisih dua sudut, dapat diperoleh rumus sebagai berikut
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
Jika ruas yang bersesuaian kita jumlahkan maka akan diperoleh
cos (A + B) + cos (A – B) = 2 cos A cos B
atau
2 cos A
cos B = cos (A + B) + cos (A – B)
c. Perkalian Sinus dan Cosinus
Dari rumus jumlah
dan selisih dua sudut, dapat diperoleh rumus sebagai berikut.
sin (A + B) = sin A cos B + cos A sin B
sin (A – B) = sin A cos B – cos A sin B
Jika ruas yang bersesuaian kita jumlahkan maka akan diperoleh
sin (A + B) + sin (A – B) = 2 sin A cos B
atau
2 sin A cos B = sin (A + B) + sin (A – B)
Sedangkan jika ruas yang bersesuaian kita kurangkan maka akan diperoleh
2 cos A sin B = sin (A + B) – sin (A – B)
Contoh:
Sederhanakanlah
sin 105° cos 15°!
Jawab:
sin 105° cos
15°
= ½ {sin (105 + 15)° + sin (105 – 15)° }
= ½ (sin 120° + sin 90)°
= ½ ( ½Ö3 + 1)
= ¼Ö3 + ½
8. Rumus penjumlahan dan pengurangan Sinus, Cosinus, dan
Tangen
a. Rumus
penjumlahan dan pengurangan sinus:
b. Rumus
penjumlahan dan pengurangan cosinus:
c. Rumus penjumlahan dan pengurangan tangen:
Contoh soal:
Hitunglah nilai
dari sin 75o + sin15o!
Jawab:
Sin 75o +
sin 15o
= 2 sin ½ (75o
+ 15o) cos ½ (75 o -15o)
= 2 sin 45
o cos 30o o
= 2 x ½Ö2 x ½Ö3
= ½Ö6
Hitunglah nilai
dari cos 75 o – cos 15 o!
Jawab:
Cos 75 o
– cos 15 o
= -2 sin ½ (75
o + 15 o ) sin ½ (75 o - 15 o)
= -2 sin 45
o sin 30 o
= -2 x ½Ö2
9. Contoh cara membuktikan identitas trigonometri
Jawab:
















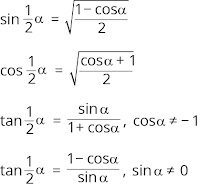



1 comments:
Write commentsmantap
Replybermanfaat ilmunya
thanks
EmoticonEmoticon