1. Pangkat Bulat positif
Definisi
Misalkan a bilangan real dan n bilangan bulat positif. Notasi an menyatakan hasil kali bilangan a sebanyak n faktor, dapat ditulis
dengan:
a sebagai basis bilangan berpangkat
n sebagai pangkat.
Catatan:
1. Pada Definisi di atas, kita sepakati, a1 cukup ditulis a.
2. Tidak semua a0 dengan a bilangan real menyatakan 1. Ketika a = 0 dan n = 0, maka an = 00, hasilnya taktentu.
3. Jika n adalah sebuah variabel sebagai eksponen dari a, maka perlu dicermati semesta variabel itu. Sebab an = a × a × ... × a sebanyak n faktor, ini hanya berlaku ketika semesta n ∈N.
Contoh:
24 = 2 x 2 x 2 x 2 =16
32 = 3 x 3 = 9
2. Pangkat Bulat Negatif
Definisi
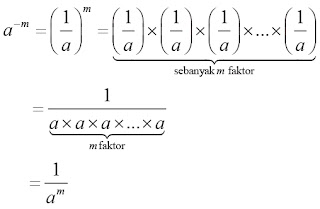
Untuk a bilangan real dan a ≠ 0, m bilangan bulat positif, didefinisikan
Definisi di atas dijelaskan sebagai berikut:
Contoh:
3. Pangkat Nol
Definisi
Untuk a bilangan real dan a ≠ 0, maka a0 = 1.
Mengapa a tidak boleh sama dengan nol?
Seperti yang telah dijelaskan diatas ketika a = 0 maka a0 = 00, hasilnya taktentu.
Contoh:
20 = 1
30 = 1
4. Sifat-sifat Pangkat Bulat Positif
Sifat-1
Jika a bilangan real, m dan n bilangan bulat positif maka
am × an = am+n
Pembuktian:
Sifat diatas hanya berlaku a bilangan real, m dan n bilangan bulat positif. Jika m dan n bukan bilangan bulat positif, Sifat-1 tidak berlaku, misalnya a = 0 dan m = n = 0, tidak berlaku.
Contoh:
Sifat-2
Jika a bilangan real dan a ≠ 0, m dan n bilangan bulat positif, maka
Pada sifat-2 tidak diizinkan a = 0, sebab bentuk perpangkatan pada Sifat-2 adalah bentuk rasional. Dalam pecahan penyebutnya tidak lazim nol. Ketika a = 0 dan m, n bilangan bulat positif, maka am atau an dimungkinkan hasilnya 0. Jika hasil am dan an keduanya nol, maka hasil baginya tak tentu. Jika am = 0 dan an ≠ 0, maka hasil baginya 0. Tetapi jika am ≠ 0 dan an = 0, maka hasil baginya tak terdefinisi.
Contoh:
Sifat-3
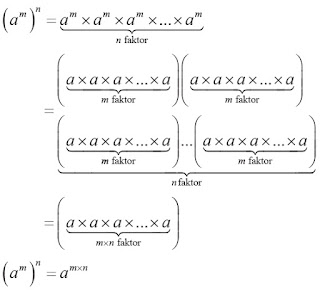
Jika a bilangan real dan a ≠ 0, m dan n bilangan bulat positif, maka (am)n = amn
Pembuktian:
Contoh:
5. Pangkat Pecahan
Definisi
Misalkan a bilangan real dan a ≠ 0, m bilangan bulat positif, maka a1/m = p adalah bilangan real positif, sehingga pm = a.
Sifat-sifat perpangkatan bilangan real dengan pangkat pecahan
Definisi
Misalkan a bilangan real dan a ≠ 0, m, n bilangan bulat positif didefinisikan
Misalkan a bilangan real dengan a > 0,
Pembuktian:
Jika a adalah bilangan real dengan a > 0,
Contoh-contoh pengerjaan soal bilangan berpangkat:
1. 53 ×5×54 = 53 ×51 ×54 = 53+1+4 = 58



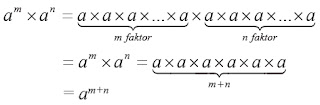



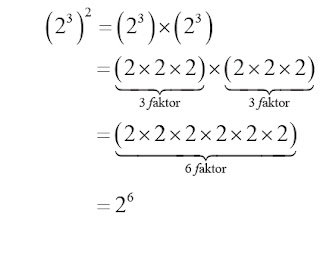





EmoticonEmoticon