Definisi Logaritma
Logaritma dituliskan sebagai “log”,
didefinisikan sebagai berikut.
Misalkan
a, b ∈ R, a > 0, a ≠ 1 , b >
0, dan c bilangan rasional,
alog b =
c jika dan hanya jika ac = b.
Contoh:
3x = 5 ⇔ x = 3log
5
5z = 8 ⇔ z = 5log 8
Bilangan pokok
(basis) 10 tidak ditulis, sehingga 10log a = log a.
Contoh:
103 = 1000 maka log 1000 = 3
Logaritma
dengan basis e (e adalah bilangan Euler, yaitu e ≈
2,718…,), maka elog b ditulis ln b.
Sifat-sifat Logaritma
Sifat dasar
Misalkan a dan n
bilangan real, a > 0 dan a ≠ 1, maka
1. alog
a = 1
alog a = x ⇔
ax = a sehingga x = 1 atau alog
a = 1
2. alog 1 = 0
alog 1 = x ⇔ ax = 1. Karena a0 = 1, maka x = 0
3. alog an =
n
alog an =
x ⇔ ax
= an sehingga x = n maka alog
an = n
Sifat operasi logaritma
4. Untuk a, b, dan c bilangan
real positif, a ≠ 1, dan b > 0,
berlaku a log (b x c) = a
log b + alog c
Pembuktian
a log b = x
⇔ b = ax
a log c = y
⇔ c = ay
Mengalikan
b dengan c
b × c = ax
× ay
b × c = ax+y
a log
(b × c) = x + y
Substitusi
nilai x dan y
a log (b × c )
= a log b + a log c
(terbukti)
5.
Untuk a,
b, dan c bilangan real dengan a > 0, a ≠ 1, dan b
> 0, berlaku
Pembuktian
a log b = x
⇔ b = ax
a log c = y
⇔ c = ay
Membagi b dengan c
6.
Untuk a, b bilangan real dan n bilangan asli, a >
0, b > 0, a ≠ 1,
berlaku a log bn = n a
log b
Pembuktian
7.
Untuk a, b, dan c bilangan real positif, a ≠ 1, b
≠ 1, dan c ≠ 1, berlaku
Pembuktian
a log b = x
⇔ b = ax
Ambil sembarang c bilangan
real, c > 0, dan c ≠ 1 sedemikian sehingga:
Karena c bilangan real dan c
≠ 1 sembarang dengan ketentuan di atas dapat dipenuhi c = b sehingga
diperoleh
8.
Untuk
a, b, dan c bilangan real positif dengan a ≠ 1 dan b
≠ 1, berlaku
a log b x b log c = a
log c
Pembuktian
a log b = x
⇔ b = ax
b log c = y
⇔ c = by
9.
Untuk a dan b bilangan real positif dengan a ≠ 1, berlaku
dengan
m, n bilangan rasional dan m ≠ 0.
Pembuktian
10.
Untuk a bilangan real positif a ≠ 1, berlaku
Pembuktian
Misalkan
Contoh
soal:
Hitunglah
1.
6 log 1
Jawab:
6 log 1 = 0
3.
32 log 8
Jawab:
4.
3 log 54 – 3 log 2
Jawab:
5.
Sederhanakanlah log 64 − log 128 + log 32
Jawab:
log 64 – log 128 + log 32
= log 26
– log 27 + log 25
= 6 log 2−7 log 2+ 5 log 2
= 4 log 2
Nyatakan dalam a, b, c. (a = log 2, b= log 3, c =
log 5)
6. log 30
Jawab:
log 30
= log (2 x 15)
= log ( 2 x 3 x 5)
= log 2 + log 3 + log 5
= a + b +c
7. log 900
Jawab:
log 900
= log ( 2 x 450)
= log ( 2 x 2 x 225)
= log ( 2 x 2 x 3 x 75)
= log (2 x 2 x 3 x 3 x 25)
= log (2 x 2 x 3 x 3 x 5 x 5)
= log (22 x 32 x 52)
= log 22 + log 32 + log 52
= 2 log 2 + 2 log 3 + 2 log 5
= 2a + 2b + 2c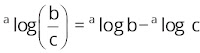
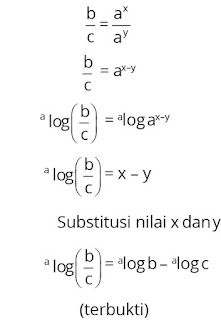
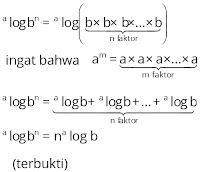







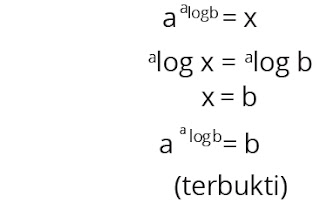



EmoticonEmoticon