Cara Menghitung Mean, Median, dan Modus

Ukuran pemusatan data

Ukuran pemusatan data merupakan ukuran statistik yang menunjukkan pusat sekumpulan data. Cara mengukur lokasi pusat data diantaranya yaitu dengan rata-rata aritmatika (mean), median, modus, rata-rata geometris, rata-rata harmonis dan rata-rata kuadratis. Masing-masing ukuran pemusatan data memiliki kelebihan dan kekurangannya sendiri. Ketepatan penggunaanya bergantung pada sifat data dan tujuan pengamatan. Untuk ukuran pemusatan data yang paling banyak digunakan adalah mean, median, dan modus.

Berikut cara menghitung mean, median, dan modus untuk data berkelompok dan data tidak berkelompok. Data berkelompok adalah data yang sudah diurutkan dalam tabel distribusi frekuensi, sedangkan data tidak berkelompok adalah data mentah dan diperhitungkan secara individual.

1. Mean (rata-rata aritmatika)

Mean atau rata-rata aritmatika atau lebih sering disebut rata-rata merupakan ukuran lokasi pusat yang paling umum digunakan dalam statistika. Kelemahan dari rata-rata aritmatika yaitu sangat dipengaruhi oleh nilai ekstrim minimum dan maksimumnya.

a. Mean data tidak berkelompok / data tunggal

Mean dari sekumpulan data yang banyaknya n adalah jumlah data dibagi dengan banyaknya data. Secara matematis mean dapat dirumuskan:

Rumus menghitung mean data tunggal/tidak berkelompok

dengan:

å x = jumlah data

N = banyaknya data

Contoh

Hasil ujian statistika 10 mahasiswa adalah sebagai berikut : 5, 7, 6, 8, 2, 6,9, 5, 7, dan 4. Berapa rata-rata dari data tersebut.

Jawab:

Rata-rata = jumlah data/banyak data = 5+7+6+8+2+6+9+5+7+4/10

Rata-rata =59/10 = 5,9

Rumus rata-rata untuk data tunggal yang telah dalam tabel distribusi frekuensi adalah

Contoh

Berdasarkan data hasil ujian statistika dua mahasiswa mendapat nilai 8, lima mahasiswa mendapat nilai 7, sebelas mahasiswa mendapat nilai 6, delapan mahasiswa mendapat nilai 5, dan sembilan mahasiswa mendapat nilai 4. Tentukan rata-ratanya.

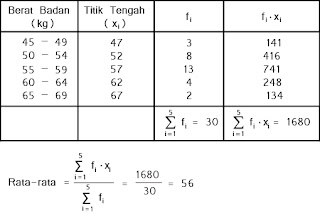
b. Rata-rata data berkelompok

Rata-rata untuk data berkelompok pada hakikatnya sama dengan menghitung rata-rata

data pada distribusi frekuensi tunggal dengan mengambil titik tengah kelas sebagai xi.

Rumus rata-rata untuk data berkelompok

Rumus menghitung rata-rata untuk data berkelompok

dengan:

f = frekuensi kelas

x = titik tengah kelas

Contoh:

Tentukanlah rata-rata dari data berikut:

Jawab:

2. Median

Median dari sekumpulan data adalah suatu bilangan yang membagi data tersebut menjadi dua bagian yang sama setelah data tersebut diurutkan dari yan lebih kecil ke yang lebih besar atau sebaliknya.

a. Median data tunggal/tidak berkelompok

Cara menentukan median untuk data tunggal adalah dengan cara menyusun data secara urut dari data terkecil sampai dengan data terbesar atau sebaliknya, kemudian nilai median ditentukan secara langsung yaitu data yang paling tengah.

Atau dengan rumus:

Rumus menghitung median untuk data tunggal

Contoh:

1)Tentukan median dari data berikut: 81, 74, 63, 85, 92.

Data diurutkan dari terkecil hingga terbesar: 63, 74, 81, 85, 92.

Jadi nilai median dari data tersebut adalah 81.

2)Tentukan median dari data berikut: 1, 2, 3, 3, 4, 4, 7, 9

Jawab:

b. Median data berkelompok

Cara menghitung median untuk data berkelompok dalam bentuk distribusi frekuensi dapat dirumuskan sebagai

letak median adalah pada data ke n/2

dengan:

n = banyak data

b = tepi bawah kelas median

p = lebar atau panjang kelas

F = Frekuensi kumulatif sebelum kelas median

f = frekuensi kelas median

contoh:

Tentukanlah median dari data berikut.

Penyelesaiannya:

Letak median adalah pada data ke 30/2 = 15

Berdasarkan tabel terlihat bahwa data ke 15 berada pada interval kelas yang mempunyai frekuensi kumulatif 17.

Contoh cara menghitung median untuk data berkelompok dalam bentuk distribusi frekuensi

Maka,

b = (69 + 70)/2 = 69,5

p = 65 – 60 = 5

F = 5

n = 30

f = 12

Sehingga Nilai mediannya

Modus

Modus adalah nilai data yang paling sering muncul atau nilai data yang mempunyai frekuensi paling tinggi. Sekumpulan data mungkin saja memiliki lebih dari satu modus atau bahkan tidak mempunyai modus jika semua data memiliki frekuensi yang sama.

a. Modus data tunggal

Nilai modus untuk data tunggal dapat ditentukan secara langsung dengan melihat frekuensi kemunculan setiap data yang paling tinggi. Sehingga untuk menghitung modus data tidak berkelompok tidak diperlukan rumus-rumus tertentu.

Contoh:

Tentukanlah modus dari data berikut: 2, 5, 6, 8, 8, 8, 9

Terlihat bahwa 8 merupakan data yang paling sering muncul, maka modusnya adalah 8.

b. Modus data berkelompok

Cara menghitung modus untuk data berkelompok dapat dirumuskan sebagai

Rumus menghitung modus untuk data berkelompok

dengan:

b = tepi bawah kelas yang memuat modus

p = panjang atau lebar kelas

d1 = frekuensi kelas modus dikurangi frekuensi kelas sebelumnya

d2 = frekuensi kelas modus dikurangi frekuensi kelas sesudahnya

kelas interval yang memuat modus adalah kelas interval yang mempunyai frekuensi paling banyak.

Kita gunakan kembali tabel sebelumnya untuk mencoba menghitung modus.

Hitunglah modus dari tabel berikut:

Contoh menghitung modus untuk data berkelompok

Jawab:

Pertama tentukan letak modusnya. Modus terletak pada kelas interval dengan frekuensi paling banyak, maka modus berada pada interval 70-74 yaitu dengan frekuensi 12.

Sehingga,

b = 69,5

l = 65 – 60 = 5

d1 = 12 -5 = 7

d2 = 12- 7 = 5

Jadi modus dari data diatas