Pengertian
Lingkaran
Lingkaran adalah tempat kedudukan atau himpunan titik-titik yang berjarak
sama terhadap suatu titik yang tertentu. Titik tertentu tersebut dinamakan
pusat lingkaran dan jarak yang tetap tersebut dinamakan jari-jari lingkaran.
Diameter lingkaran adalah ruas garis yang panjangnya dua kali jari-jari
lingkaran dan melalui pusat lingkaran.
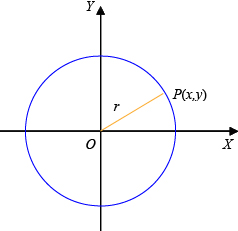
Jika titik
P terletak
pada lingkaran yang berpusat di O,
maka berlaku OP = jari-jari
lingkaran. Dengan menggunakan rumus jarak titik O(0, 0) ke titik P(x ,
y) diperoleh:
Karena jarak
antara O dan P adalah jari-jari lingkaran maka
Karena titik
(x,y) adalah sembarang titik pada lingkaran, maka setiap titik pada lingkaran
berlaku x2 + y2 = r2 . Jadi persamaan
lingkaran dengan pusat O(0,0) dan
berjari-jari r adalah
Berikut contoh
soal agar lebih memahami tentang cara menentukan persamaan lingkaran berpusat
di O(0, 0).
Contoh soal
Contoh soal
1.Tentukan
persamaan lingkaran jika diketahui pusatnya O(0, 0) dan berjari-jari 4.
Jawab:
Persamaan lingkaran
yang berpusat di O(0, 0) dan r = 4 yaitu
x2 + y2
= r2
x2 + y2
= 42
x2 + y2
= 16
Jadi, persamaan
lingkaran dengan pusat di O(0,
0) dan r = 4 adalah
x2 + y2
= 16
2. Tentukan
persamaan lingkaran jika diketahui pusatnya O(0, 0) dan melalui (9, –12).
Jawab:
Jadi, persamaan
lingkaran dengan pusat di O(0,
0) dan melalui (9, –12) adalah
x2 + y2
= 225
Persamaan
Lingkaran Berpusat di Titik A(a, b)
Jika titik A(a, b) adalah pusat
lingkaran dan titik B(x, y) terletak pada lingkaran, maka jari-jari lingkaran r sama dengan jarak dari A ke B.
r = AB
r2 = (AB)2
r2= (xB – xA)2 + (yB – yA)2
r2 = (x – a)2 + (y – b)2
Jadi persamaan
lingkaran yang berpusat di (a, b) dan berjari-jari r adalah
Contoh
Tentukan persamaan
lingkaran yang pusatnya (–3, 4) dan berjari-jari 7;
Jawab
Persamaan
lingkaran:
(x – (–3))2 + (y – 4)2 = 72
(x + 3)2 + (y – 4)2 = 49
x2 + 6x + 9 + y2 – 8y + 16 = 49
x2 + y2 + 6x – 8y + 25 = 49
x2 + y2 + 6x – 8y – 24 = 0
2. Tentukan
persamaan lingkaran yang pusatnya (7, 3) dan melalui (-2, 1);
Jawab:
Hitung jari-jarinya terlebih dahulu
Hitung jari-jarinya terlebih dahulu
Bentuk umum persamaan lingkaran
Berdasarkan
persamaan lingkaran dengan pusat (a,
b) dan berjari-jari r adalah:
(x – a)2 + (y – b)2 = r
x2 – 2ax + a2 + y2 – 2by + b2 = r2
x2 + y2 – 2ax – 2by + a2 + b2 = r2
x2 + y2 – 2ax – 2by + a2 + b2 – r2 = 0
Jika –2a = 2A, –2b = 2B dan a2 + b2 – r2 = C, maka diperoleh bentuk umum persamaan
lingkaran:
dengan:
pusatnya (–A, –B)
jari-jari lingkaran
Menentukan Pusat
dan Jari-Jari Lingkaran yang Persamaannya Diketahui
Contoh soal
Tentukan koordinat
pusat dan panjang jari-jari lingkaran jika persamaan lingkaran tersebut
x2 + y2 +8x – 2y + 8 = 0
Jawab:
Pertama bandingkan
bentuk persamaan lingkaran tersebut dengan bentuk umum persamaan lingkaran
x2 + y2 – 8x – 2y + 8 = 0
x2 + y2 + 2Ax + 2By + C = 0
Maka diperoleh:
2A = 8
A = 4
2B = –2
B = -1
C = 8
Ingat pusat
lingkaran merupakan (–A,-B), maka pusat lingkarannya (-4, 1).
Sekarang
menghitung jari-jari lingkaran,
Jadi, pusat lingkaran
(-4, 1) dan jari-jari lingkaran = 3.
Kedudukan Titik
terhadap Lingkaran
Posisi titik P(x1, y1)
terhadap lingkaran dapat diketahui hanya dengan mengetahui jarak titik P(x1, y1)
ke pusat lingkaran. Berdasarkan jarak titik ke pusat lingkaran, ada 3
kemungkinan posisi titik terhadap lingkaran.
1. Titik P(x1, y1)
berada di dalam lingkaran jika jarak titik P(x1,
y1) ke pusat
lingkaran kurang dari jari-jari lingkaran.
2. Titik P(x1, y1)
berada pada lingkaran jika jarak titik P(x1, y1)
ke pusat lingkaran sama dengan jari-jari lingkaran.
3. Titik P(x1, y1)
berada di luar lingkaran jika jarak titik P(x1,
y1) ke pusat
lingkaran lebih besar dari jari-jari lingkaran.
Posisi Titik P(x1, y1)
terhadap Lingkaran x2
+ y2 = r2
Jika x12 + y12 < r2 , maka titik P(x1, y1)
terletak di dalam lingkaran.
Jika x12 + y12 = r2 , maka titik P(x1, y1)
terletak pada lingkaran.
Jika x12 + y12 > r2 , maka titik P(x1, y1)
terletak di luar lingkaran.
Contoh
Tentukan posisi
titik A(3, 4) , B(–8,
6), C(8, –9) terhadap lingkaran
x2 + y2 = 100.
Jawab:
A(3, 4)
x2 + y2 = 32
+ 42 = 9 + 16 = 25
25 < 100
Jadi titik A(3, 4) terletak di dalam lingkaran x2 + y2 = 25.
B(–8, 6)
x2 + y2 = (-8)2
+ 62 = 64 + 36 = 100
100 = 100
Jadi B(–8, 6) terletak pada lingkaran x2 + y2 = 100.
C(8, 9)
x2 + y2 = 82
+ 92 = 64 + 81 = 145
145 > 100
Jadi C(–8, 6) terletak di luar lingkaran x2 + y2 = 100.
Posisi Titik P(x1, y1) terhadap
Lingkaran (x – a)2 + (y – b)2 = r2
Jika (x1 – a)2 + (y1 – b)2 < r2 , maka titik P(x1, y1) terletak
di dalam lingkaran.
Jika (x1 – a)2 + (y1 – b)2 = r2 , maka titik P(x1, y1) terletak
pada lingkaran.
Jika (x1 – a)2 + (y1 – b)2 > r2 , maka titik P(x1, y1) terletak
di luar lingkaran.
Contoh
Tentukanlah posisi
titik A(5, 1)terhadap lingkaran
dengan persamaan x2
+ y2 – 4x + 6y – 12 = 0.
Jawab:
Persamaan
lingkaran x2 + y2 – 4x + 6y – 12 = 0 dapat diubah
sebagai berikut.
x2 + y2 – 4x + 6y – 12 = 0
(x2 – 4x) + (y2 + 6y)
– 12 = 0
Kedua ruas ditambah
13 (ditambah 4 kemudian ditambah 9 agar persamaan tersebut dapat
disederhanakan)
(x2 – 4x + 4) + (y2 + 6y +
9) – 12 = 13
(x – 2)2 + (y + 3)2 – 12 = 13
(x – 2)2 + (y + 3)2 = 25
Koordinat titik A (4, 1) maka
(4 – 2)2
+ (1 + 3)2 = 4 + 16 = 20
20 < 25
Jadi titik A (4, 1) terletak di dalam lingkaran.
Posisi Garis
terhadap Suatu Lingkaran
Berdasarkan
determinannya, ada 3 kemungkinan posisi garis terhadap suatu lingkaran:
Jika D< 0 maka
garis terletak di luar lingkaran dan tidak memotong lingkaran. Jarak pusat
lingkaran ke garis lebih besar dari jari-jari lingkaran (k > r).
Jika D = 0, maka
garis terletak pada lingkaran dan memotong lingkaran di satu titik. Jarak pusat
lingkaran ke garis sama dengan jari-jari lingkaran (k = r).
Jika D > 0,
maka garis akan melewati bagian dalam lingkaran dan memotong lingkaran di dua
titik. Jarak pusat lingkaran ke garis lebih kecil dari jari-jari lingkaran (k < r).
Contoh:
Tentukan apakah
garis x – y + 1 = 0 memotong lingkaran x2 + y2 = 49!
Jawab:
x – y + 3 = 0 ⇒ y = x + 3 ….. (1)
x2 + y2 = 49 ……(2)
subtitusikan persamaan
(1) ke persamaan (2):
x2 + y2 = 49
x2 + (x + 3)2 = 49
x2 + x2 + 6x + 9 = 49
x2 + x2 + 6x + 9 – 49 = 0
2x2 + 6x – 40 = 0
x2 + 3x – 20 = 0
D = b2 – 4ac
= 32 –
4 ⋅ 1 (–20)
= 1 + 80
= 81 > 0
Karena D > 0,
maka garis x – y + 3 memotong lingkaran x2 + y2 = 49 di dua titik yang
berbeda.
Persamaan Garis Singgung Lingkaran
1. Persamaan Garis Singgung yang Melalui Suatu Titik pada Lingkaran
a. Persamaan Garis Singgung di Titik P (x1,
y1) pada Lingkaran x2 + y2 = r2
Contoh soal:
Tentukan persamaan
garis singgung pada lingkaran x2 + y2 = 25 di titik
(3, –4).
Jawab:
Persamaan garis
singgung di titik (3, -4) pada lingkaran x2 + y2 = 25 adalah:
x1x + y1y
= r2
3x – 4y = 25
b. Persamaan Garis Singgung Melalui Titik (x1, y1)
pada Lingkaran
(x – a)2
+ (y – b)2 = r2
Persamaan garis
singgung pada Lingkaran (x – a)2 + (y –
b)2 = r2
c. Persamaan Garis Singgung Melalui Titik Q(x1,
y1) pada Lingkaran
x2 + y2 + 2Ax + 2By + C = 0
Maka persamaan
garis singgung melalui Q(x1, y1) pada lingkaran x2
+ y2 + 2Ax +
2By + C = 0 adalah
2. Persamaan Garis Singgung
Lingkaran melalui titik diluar lingkaran
Persamaan garis singgung lingkaran melalui titik A(x1,
y1) di luar lingkaran. Jika melalui titik A(x1,
y1) di luar lingkaran ditarik dua buah garis singgung pada lingkaran
dengan titik singgungnya B(x2, y2)
dan C(x3, y3), maka persamaan garis BC
adalah x1x + y1y = r2
disebut garis kutub pada lingkaran dan titik A(x1, y1)
disebut titik kutub.
Cara menentukan Persamaan
garis singgung lingkaran melalui titik A(x1, y1)
di luar lingkaran adalag dengan membuat persamaan garis kutub dari titik A(x1,
y1) terhadap lingkaran. Kemudian membuat persamaan garis
singgung melalui titik potong garis kutub dan lingkaran.
Contoh:
Tentukan persamaan
garis singgung melalui titik (3, 1) di luar lingkaran x2 + y2
= 2
Jawab:
Persamaan garis
kutub di (3, 1) adalah sebagai berikut:
x1x + y1y
= r2
3x + 1y = 2
y = 2 - 3x
y = 2 – 3x
Persamaan garis y
= 2 – 3x disubstitusikan dengan lingkaran x2 + y2
= 16 diperoleh:
x2 + y2
= 4
x2 + (2 – 3x)2=
16
x2 + 4 – 12x +
9x2 = 16
10x2 – 12x + 4
= 2
10x2 – 12x + 2
= 0
5x2 – 6x + 1 = 0
5x2 – 5x - x + 1 = 0
5x(x-1)-1(x-1)
(5x-1)(x-1)= 0
5x-1 = 0 maka x =
1/5
Atau
x-1 = 0 maka x = 1
Untuk x = 1/5,
maka y = 2
– 3x
= 2 – 3 ⋅ 1/5
= 2 – 3/5
= 7/5
Diperoleh titik
singgung (1/5, 7/5).
Jadi, persamaan
garis singgung melalui (1/5, 7/5) adalah 1/5x + 7/5y = 2 atau
juga dapat dituliskan x + 7y = 10.
Untuk x =
1,
maka y = 2 – 3x
= 2 – 3.1
= 2 – 3
= –1
Diperoleh titik
singgung (1, –1).
Jadi, persamaan
garis singgung melalui (1, –1) adalah x – y = 2.
3. Persamaan Garis Singgung
yang Gradiennya Diketahui
a. Persamaan Garis Singgung dengan Gradien m terhadap Lingkaran
x2 + y2 = r2
Jadi, persamaan garis singgung dengan gradien m pada
lingkaran x2 + y2 = r adalah:
b. Persamaan Garis Singgung dengan Gradien m terhadap Lingkaran
(x – a)2 + (y
– b)2 = r2
Maka persamaan
garis singgung dengan gradien m terhadap lingkaran (x – a)2
+ (y – b)2 = r2 adalah:
c. Persamaan Garis Singgung dengan Gradien m terhadap Lingkaran
x2 + y2
+ 2Ax + 2By + C = 0
Untuk menentukan
persamaan garis singgung gradien m terhadap lingkaran x2 + y2 +
2Ax + 2By + C = 0 dapat dilakukan dengan cara mengubah
dahulu ke bentuk (x – a)2 + (y – b)2
= r2 sehingga persamaan garis singgungnya sama.


















EmoticonEmoticon