Limit
secara intuitif limit dapat didefinisikan sebagai berikut:
Sifat-sifat
limit fungsi
Misal k suatu konstanta, f dan g adalah
fungsi-fungsi yang mempunyai limit untuk x mendekati c. Sifat-sifat
pokok limit fungsi tersebut yaitu:
* sumber : calculus. Verberg- Purcell- Rigdon
Contoh soal dan pembahasannya:
1. Tentukan 
!
!
Jawab:
Untuk menentukan nilai limit tersebut, pertama kita
gunakan sifat ke 4 dari sifat-sifat limit yang ada pada gambar di atas.
Sehingga hasilnya
Selanjutnya gunakan sifat ke 3, maka menjadi
Langkah terakhir gunakan sifat ke 2 (untuk sebelah kiri
tanda penjumlahan) dan sifat 1 (untuk sebelah kanan tanda penjumlahan, hasilnya
akan sebagai berikut
2. Tentukan
!
!
Jawab:
Langkah pertama gunakan sifat 5, sehingga
Berikutnya adalah dengan sifat 3,
Kemudian gunakan sifat 8,
Selanjutnya gunakan sifat 2 dan 1,
3. Tentukan 
!
!
Jawab:
Dengan menggunakan cara yang sama seperti di atas,
diperoleh
4. tentukan 
!
!
Jawab:
Cara Menghitung limit dengan cara subtitusi
Hal-hal yang perlu diperhatikan dalam subtitusi nilai
limit adalah sebagai berikut:
Akan tetapi tidak semua soal limit dapat dipecahkan
langsung dengan cara subtitusi. Terkadang jika disubtitusi akan dihasilkan
bentuk
Jika demikian, maka kita harus menyederhanakan bentuk
limit tersebut terlebih dahulu hingga jika kita subtitusikan tidak menghasilkan
bentuk 0/0.
Contoh soal:
1. tentukan limit dari 
!
!
Jawab:
2. tentukan limit dari 
!
!
Jawab:
3. Tentukan limit dari 
!
!
Jawab:
4. Tentukan limit dari
!
!
Jawab:
Karena menghasilkan bentuk 0/0, maka perlu disederhanakan
terlebih dahulu.
Untuk bentuk tersebut kita sederhanakan dengan cara
difaktorkan. Sehingga
5. tentukan limit dari 
!
!
Jawab:
Karena menghasilkan bentuk 0/0, maka perlu disederhanakan
terlebih dahulu.
Untuk bentuk seperti di atas perlu dikalikan dengan
sekawannya. Sehingga
Cara Menghitung Limit Fungsi Trigonometri
Sifat-sifat limit fungsi trigonometri
Berikut sifat-sifat limit fungsi trigonometri.
Teorema:
*sumber: calculus karya Verberg, Purcell, dan Rigdon.
Sifat-sifat istimewa limit fungsi trigonometri.
Berikut ini adalah sifat-sifat istimewa limit fungsi
trigonometri:
Contoh soal limit fungsi trigonometri:
1. Tentukan nilai dari
!
!
Jawab:
2. Berapakah nilai dari 
!
!
Jawab:
3. Hitunglah nilai dari
!
!
Jawab:
Limit di
tak hingga
Definisi
Jika f fungsi yang terdefinisi pada sembarang interval
(a,¥). Maka
Untuk x positif yang besar sekali, maka nilai f(x)
mendekati L
Jika f fungsi yang terdefinisi pada sembarang interval (-¥,b).
Maka
Untuk x negatif yang turun sekali, maka nilai f(x)
mendekati L
Cara menyelesaikan soal Limit tak hingga
Untuk menyelesaikan limit fungsi tak hingga bentuk
dapat diselesaikan dengan cara membagi pembilang dan penyebut dengan pangkat
tertinggi yang ada pada pembilang atau penyebut. Misalkan x dengan pangkat
tertinggi yang ada pembilang alalah x2 dan x dengan pangkat
tertinggi pada penyebut adalah x3, karena x dengan pangkat tertinggi
adalah x3 maka baik pembilang dan penyebut dibagi dengan x3.
Untuk lebih jelasnya silahkan perhatikan contoh yang ada dibawah.
Sifat-sifat limit tak hingga
Sebelum masuk ke contoh soal limit tak hingga, kita
terlebih dahulu sedikit membahas tentang sifat-sifat limit tak hingga.
Jika suatu limit fungsi tak hingga bentuk
dibagi
dengan pangkat tertinggi yang ada pada pembilang atau penyebut maka akan
memiliki sifat:
Contoh soal limit tak hingga:
1. tentukan nilai dari 
!
!
Jawab:
Karena x pangkat tertinggi adalah x2 maka
pembilang dan penyebut dibagi dengan x2
2. Tentukan nilai dari
!
!
Jawab:
* 0 pada 7/0 bukan angka
nol tetapi angka yang kecil sekali sehingga suatu bilangan dibagi kecil sekali
hasilnya besar sekali atau ∞ .
3. Tentukan nilai dari
!
!
Jawab
Semoga Contoh Pengerjaan Soal-soal tentang limit di atas
bermanfaat untuk kalian
Dan jangan lupa like
and share ya!
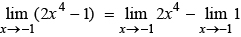
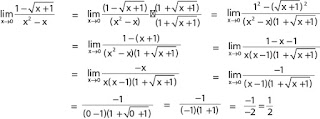
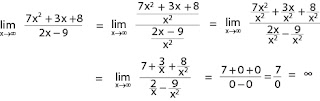
EmoticonEmoticon