Menentukan Sisa Pembagian Suku Banyak oleh Bentuk (x – k),
Dalam menentukan sisa pembagian suku banyak oleh bentuk linear, kita dapat menggunakan teorema sisa.
Jika suku banyak f(x) dibagi (x – k), maka sisa pembagiannya adalah f(k).
Penjelasan dari teorema tersebut adalah sebagai berikut.
Diketahui f (x) = (x – k) h(x) + S.
dengan:
f(x) = suatu suku banyak
(x – k)= pembagi suku banyak
h(x) = hasil bagi
S = sisa pembagian suku banyak
Derajat S lebih rendah satu daripada derajat (x – k), sehingga S merupakan konstanta.
Karena f(x) = (x – k) k(x) + S berlaku untuk semua x,
maka jika x disubtitusi dengan k akan diperoleh:
f (k) = (k – k) h(k) + S
= 0 ⋅ h(k) + S
= 0 + S
= S
Jadi f(k) = S dan S merupakan sisa pembagian.
Contoh soal:
Tentukanlah sisa pembagian dari f(x) = x3 + 5x2 + 2x + 8 dibagi (x - 2).
Jawab:
Pengerjaan dengan menggunakan teorema sisa
f(x) = x3 + 5x2 + 2x + 8
f(2) = (2)3 + 5(2)2 + 2.2 + 8
= 8 + 20 + 4 + 8
= 40
Jadi sisa pembagiannya adalah 40.
Sekarang kita coba kerjakan soal diatas dengan metode horner.
Jika dikerjakan dengan skema horner akan diperoleh:
Jadi kedua cara tersebut akan menghasilkan hasil yang sama. Pilihlah cara pengerjaan yang menurut kalian lebih mudah.
Menentukan Sisa Pembagian Suku Banyak oleh Bentuk (ax + b)
Teorema
Mengapa bisa demikian? Berikut penjelasannya
Jadi dapat disimpulkan bahwa sisa pembagiannya adalah f(- b/a).
Contoh soal:
Tentukan sisa pembagian dari f(x) = 8x3 + 8x2 + 4x – 5 dibagi (2x + 1).
Jawab:
Pertama kita coba kerjakan dengan teorema diatas, hasilnya:
Jika dikerjakan dengan metode horner, hasilnya:
Menentukan Sisa Pembagian Suku Banyak oleh Bentuk Kuadrat
Untuk menentukan sisa pembagian suku banyak oleh bentuk kuadrat, kita dapat menggunakan teorema sisa berikut ini.
Jika suatu suku banyak f(x) dibagi (x – a)(x – b)
maka sisanya adalah px + q
dengan:
f(a) = pa + q
f(b) = pb + q
contoh:
Jika f(x)= x3 - 6x2 + 8x –3 dibagi x2 - 5x + 6, tentukanlah sisa pembagiannya.
Jawab:
bentuk x2 - 5x + 6 dapat difaktorkan menjadi (x - 2)(x – 3).
Berdasarkan teorema di atas maka perhitungannya sebagai berikut.
(x - 2)(x – 3)
dibandingkan bentuk tersebut dengan bentuk (x – a)(x – b),
maka nilai a = 2 dan b = 3.
Selanjutnya adalah mensubtitusikan nilai a dan b ke persamaan f(a) dan f(b)
f (a) = pa + q
f (2)= 2p + q
ingat bahwa f(x)= x3- 6x2 + 8x -3, maka f(2)= 23–6(2)2+8(2)–3.
sehingga
(2)3 – 6(2)2 + 8(2) – 3 = 2p + q
8 – 24 + 16 – 3 = 2p + q
–3 = 2p + q ……… persamaan 1
f (b) = pb + q
f (3)= 3p + q
(3)3 – 6(3)2 + 8(3) – 3 = 3p + q
27 –54 + 24 – 3 = 3p + q
–6 = 3p + q ………persamaan 2
Langkah selanjutnya adalah menghitung nilai p dan q dengan cara eliminasi persamaan 1 dan 2.
Nilai p disubtitusikan ke persamaan 1
–3 = 2p + q
–3 = 2(-3) + q
–3 = -6 + q
q = 3
Jadi sisa pembagiannya = px + q = -3x + 3
Semoga Contoh Cara Menghitung Sisa Pembagian Suku Banyak dengan Teorema Sisa di atas bermanfaat untuk kalian
Dan jangan lupa like and share ya!



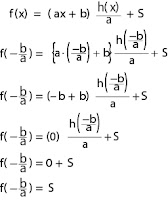
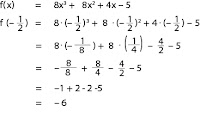


EmoticonEmoticon